Accurate modeling of a gear

[PEC]

It was not supposed to be a tutorial on gear’s tooth modeling… but one thing involving the next one, who knows
Of course, there are many gears generators (Free Gear Generator - Design & Create Spur Gears – Evolvent Design), but if you want to know what’s behind the scene…

To define a “standard” gear, you need only a few parameters:

• radius or diameter D, which define the Reference circle
• teeth number Z
• modulus number m = D/Z
• pressure angle alpha : this is standardized to 20° or 25°

The first 3 parameters are not independent, as they are related by the relation m = D/Z. Note that D and m are in the same unit, mm or inch, and that m is a distance. I will use mm.

The modulus number m defines the geometry of the teeth, and for 2 gears to be compatible, they must have:

• the same modulus m, and
• the same pressure angle alpha

Then the shape of the teeth is normalized:

• the teeth extend m mm above the Reference circle, up to the Tip Circle
• the teeth go down 1.25*m mm below the Reference circle, down to the Root circle
• along the Reference circle, the width of the teeth is equal to the space between 2 consecutive teeth

Now, what does the pressure angle alpha mean?
We often think of 2 gears as cylinders rolling without sliding in opposite direction:

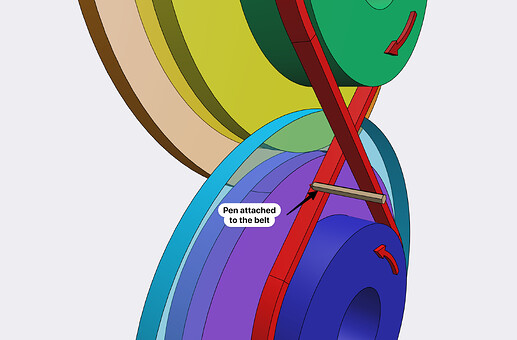
But we can also think of 2 smaller pulleys connected by a belt in the shape of 8:

The belt define the angle alpha with the line tangent to both cylinders D1 and D2. This is the pressure angle alpha of the gear. It is normalized to 20° or 25°. I will use 20° which is the most commun value. The direction of the straight portion of the belt is the pressure line.

The diameter of the smaller pulley defines the Base circle that will be used later on, and by construction, the Base circle is tangent to the pressure line.

Now, what should the shape of the teeth be so the gear “works”?
Well, imagine that you glue a pen to the belt, so the pen can draw on the light blue and violet portion of the disk, while everything is in mouvement.

The curve drawn is named involute of the circle of the pulley.
This is the curve traced by a pencil attached to a stretched wire, which is wound around a cylinder.

Well, if the shape of the teeth is equal to the involute of the base circle for each gear, the contact between the teeth of the 2 gears will follow the straight portion of the 8 shape belt.
This curve has a lot of very nice mathematical properties, which are the reason why gears works so well, but it is not the purpose of this post to elaborate on them.

How to draw the involute of a circle?
The equation of the involute of a circle is simple, but if we don’t want to do maths, the easiest way is to approximate the circle by a polygon and to “unfold” the polygon step by step:

• step 1 : disconnect the end of segment 1 of the polygon
• step 2 : “unfold and stretch the wire” means aligning segment 1 with segment 2, or make them tangent; we now have 2 points of the involute of the circle, marked by the small crosses on the figure
• step 3 : “unfold a bit more and stretch the wire” means aligning segment 1 and 2 with segment 3, or make segment 2 and 3 tangent
• repeat the process as long as needed
• connect the crosses to get the curve

So, now we have everything to draw the shape of a tooth

Here is the recipe
We kwow Diameter D, which defines the Reference circle and either the number of teeth Z or the modulus m.

• 1. offset the Reference circle by +m to draw the Tip circle
• 2. offset the Reference circle by -1.25m to draw the Root circle
• 3. draw the Pressure line inclined with an angle of alpha = 20°
• 4. draw the Base circle to be tangent to the Pressure line
• 5. draw the Involute of the Base circle using polygon approximation, until it crosses the Tip circle, and create a nice 3 points control spline to make a smooth curve
• 6. draw a radius from the center of the gear to the intersection point of the Involute of the Base circle and the Reference circle
• 7. draw a radius with an angle of ∆/4 related to the previous radius (ex: Z=20 teeth, ∆=360/20=18°, ∆/4=18/4=4.4°). This is the symmetry line of the tooth.
• 8. mirror the Involute of the Base circle relative to the previous radius to build the second side of the tooth
• 9. draw 2 radius from the center of the gear to the end of the Involute of the Base circle to complete the shape of the tooth
• 10. optionally, as the tooth is slightly rotated by a small angle (this is inherent to the construction method), simply measure this angle and rotate everything to get the construction cleaner

Then, you have the profile of a tooth, ready to be extruded (spur gear) or revolved (helicoidal gear). It is better to add a fillet to the tip and root to avoid sharp angles.

To complete the gear, all you need is to use Circular pattern to create the rest of the teeth and union it with the body of the gear.

Once you have made the first gear, you can reuse the Involute of the Base circle, you just have to scale it relative to the center of the gear with the ratio of diameter of the gears.

Gear is actually way more complex than what I explained, but if you stay in the normal range of diameter and teeth number (more than 16 teeth), you will never encounter issues.

If you want to 3D print gears, it is wise to provision for clearance by simply offsetting the Involute of the base circle by let say 0.2mm. No need to provision clearance for the tip of the tooth, as the Root circle already takes some into account with the *1.25m factor if m is in the range of 1mm or more.

I will post a few videos later on to demonstrate the recipe in action if I can make them small enough.

Good modeling

PEC

[Laci_K]

Great post @PEC , thanks for sharing! Always nice to see when someone really knows what they are talking about

[Justquestions]

Can you explain all this but in a video .

[TigerMike]

Totally agree, excellent post! I work with gears all the time and you’ve offered a great explanation. I’m not sure if there is any specification difference between metric and SAE gears. I mention that because the standard pressure angle options I’m aware of are 14.5° and 20°. I use the latter for all my work.

[PEC]

As an exemple, here is a video showing the modeling of a gear with the following caracteristics:

• diameter D = 40mm, (radius = 20mm)
• teeth number Z = 20
• modulus m = D/Z = 40/20 = 2mm
• pressure angle alpha = 20°

As you can see at the end of the video, the two gears mesh perfectly.

Edit : the video is now with the tutorial mode on, so it is easier to understand each step.

[Laci_K]

Nice video!

Just one tip, for these to be even more useful, you can turn on tutorial mode in the Settings, which would show where you tap with the pencil and fingers. (need an app restart before it applies)

[PEC]

Hi Laci,

You are right, that would be nice indeed, but I can’t find the option in the settings on the 5.340.0.4957 version of the app on the iPad. Looks like the option is missing?

I can see it on my Mac on 5.340.0.4939 version of the App (not exactly the same as the iPad ) , but I would prefer to do the video again on the iPad.

Best
PEC

[TigerMike]

The setting is not in the app. Go to iOS Settings → Shapr3D. There you can set to tutorial mode.

[PEC]

Many thanks, Mike!

I can draw gears but I can’t find this option .

So, now I found it with your help, I will redo the video

BTW, on your other remark, I only use 20°, but I was aware of 25° and thought that 14.5° was for legacy gears?

[Laci_K]

Ah, sorry I wasn’t clear, as @TigerMike said, on iPad it’s in the OS Settings.

[PEC]

No worry,
I re-did the video and edit the previous post.

As I’m with the iPad, I will record 2 more videos, showing how to reuse the involute curve to draw an other gear, and how to create an internal ring gear : there is a little trap as the Tip circle and the Root circle are reversed compare to standard gear.

[PEC]

This video shows how to create a second gear reusing the involute of the circle from the first 40mm diameter gear.

This second gear will match the first one, so we must have modulus m=2 and the pressure angle alpha = 20°.
As both the pressure angle and the modulus are the same, the new involute of the new base circle is simply the scaling of the previous curve by the ratio of the diameters.

Let say we want a 60mm diameter gear.

• D = 60mm
• m = 2mm (same as the first gear)
• m = D/Z or Z = D/m so Z = 60/2 = 30 teeth

So, we will just have to scale the involute of the circle by a ratio of 60/40 = 1.5.

For ease of drawing, I rotated the tooth profile by 90° to avoid to draw lines over the first profile.

Note also that the teeth number is 30 for this second gear, and the angle between two teeth is now 360/30 = 12° instead of 360/20 = 18° for the previous gear.

[Stephen]

That’s really helpful information PEC. Thanks for taking the time to put it together for us.

[TigerMike]

I concur with @Stephen, this is really helpful.

@PEC, thanks for clarifying the pressure angle. I guess I consider myself ‘legacy’ as well
I’ve always known about 14.5° vs 20°, and as I said, I’ve always used 20°. In fact, McMaster Carr offers 14.5° and 20° in their gear selection. I did a quick online check and here’s an excerpt from an article I found. There are several different pressure angles that can be used. Again, thanks for the education.
-Mike

[PEC]

Many thanks for sharing the article Mike, I learnt things reading it.

@Stephen : thanks for your kind words. It was fun doing the drawings and the animations, as everything is original material created just for this post:

• the 4 rotating gears are actually the one created on the videos, exported in 3mf and animated using openSCAD
• the 2 pulleys and the belt are pictures exported from Shapr3D. The animation of the pen drawing on the rotating disk is just image per image creation with Shapr3D, exported one per one and merged into an animated GIF
• the animation of the involute of the circle is done with Grapher on Mac, I wrote the equations in parametric form so the software animates them
• and the picture showing the gears teeth parameters is simply an export of 2 gears and a sketch with Shapr3D, with annotations added.

I’m always amazed by the incredible tools that are available today, I whish I had them when I studied mechanics 30 years ago

[PEC]

Last video of this first series: design of an internal ring gear.

Again, modulus and pressure angle are imposed to be 2mm and 20° so the new gear will match the previous ones:

• I choose Diameter D = 80mm
• so Z=D/m = 80/2 = 40 teeth
• the angle Delta between 2 teeth is 360/40 = 9°

As it is an internal ring gear, there is a small trap : the Tip circle is the inner circle and the Root circle is the outer circle, which is the opposite of the standard gear of the previous videos. This is an important point, as if we miss it, the gears won’t mesh.
Note also that the shape of the teeth is concave for internal ring gear instead of convex for standard gear, so the symmetry line is created accordingly.

I reused the involute of the circle drawn for the first gear:

• rotated by 180° so there is no line crossings the previous profiles during the construction process
• scaled by the ratio of the diameter (or ratio of the radius) : 80/40 = 2

The rest is straightforward.

[Stephen]

Thanks again PEC.

[PEC]

Rack design is just a special case of gear, but it is worth looking at it.

I we look what’s happen to the teeth shape when we increase the diameter of a gear for a given modulus, we got the following result:

So, a rack is simply a standard gear with a very large (infinite) diameter.
We can see on the animation that the shape of the teeth is transitioning from the convex shape to a straight line, so in the end, the shape of the teeth becomes trapezoidal.

The Reference circle, Tip circle and Root circle are becoming bigger and bigger until they also become straight lines, defining respectively Reference line, Tip line and Root line.

The distance between 2 consecutive teeth is the Pitch P of the rack.
Actually, for a given modulus, the pitch P is the same for all the gears and all the racks, as it is simply the length of the Reference circle divided by the number of teeth Z, and both quantities are proportional.

For a gear, the pitch P is the length of an arc, and for a rack it is the length of a straight line.
In both cases, P = PI * m = 3.14 * m

As for a gear, the teeth of a rack:

• extend m mm above the Reference line up to the Tip line
• extend 1.25m mm below the Reference line down to the Root line
• the width of the teeth is equal to the space between to consecutive teeth at the Reference line
• it is better to place a fillet at the tip and root edges to avoid sharp edges
• it is wise to provision for clearance if the part is intended to be manufactured.

The angle of the rack’s teeth is equal to the pressure angle Alpha, this is because of a nice property of the involute of a circle that states the contact point between the teeth of 2 gears are always located along the pressure line and that the profile of the teeth at the contact point are always perpendicular to the pressure line.

So, we have now all the elements to draw the exact profile of a rack for a given modulus m and a pressure angle alpha.

On the video, I use the same values as before:

• modulus = 2mm, so the pitch P = PI * m = 3.14 * 2 = 6.28mm
• pressure angle alpha = 20°

Looks like this post is turning more and more into a tutorial on gears using the minimum possible maths

[NathanD]

This is incredible and very useful.
Excellent work @PEC
I’ll be re-reading this thread more than a few times.

[809iLink]

Hey Pec, thanks for showing us how this works. But could you tell me how you animate those gears?